Li'l Book of Perspective

Welcome to Ivy Allie's Li'l Book of Perspective! Whether you're new to perspective drawing and looking for a simple introduction, or you're experienced with perspective and in need of a convenient reference guide, let this be your one-stop shop for perspective techniques!

For your convenience, the entire text of the guide is provided on this webpage, but you can get it in a nicer layout by downloading a PDF version. Choose from a basic PDF, or as a PDF formatted for booklet printing!

Cover of Ivy Allie's Li'l Book of Perspective

This project is distributed under a non-copyright license, so it can be redistributed for any non-commercial purposes. See the indicia for more information.

The Horizon Line
Single-Point Perspective
Two-Point Perspective
Three-Point Perspective
Ellipses
Placing Your Vanishing Points
Vanishing Points Beyond the Edge of the Page
Creating a Perspective Grid
Dividing Space
Multiplying Space
Orthographic Drawing
Faking It
Two Last Things
Exercises
Further Reading
Indicia

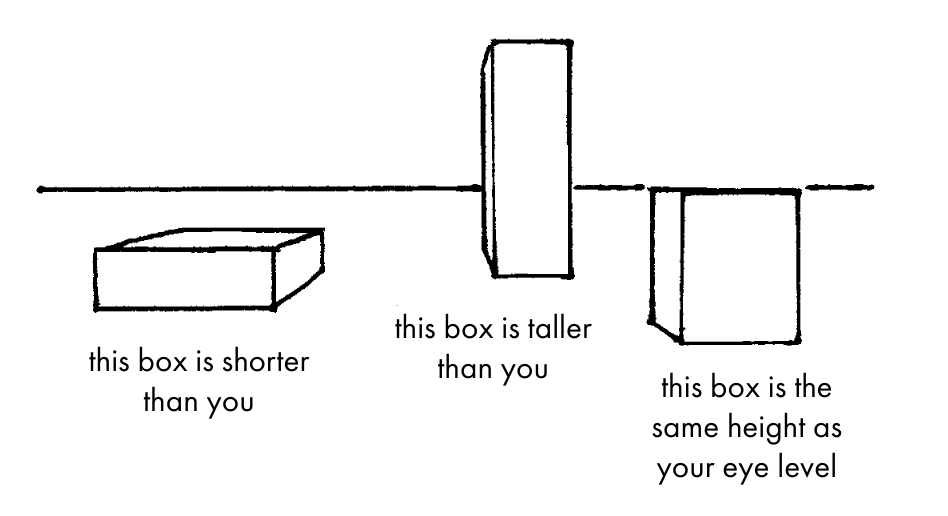
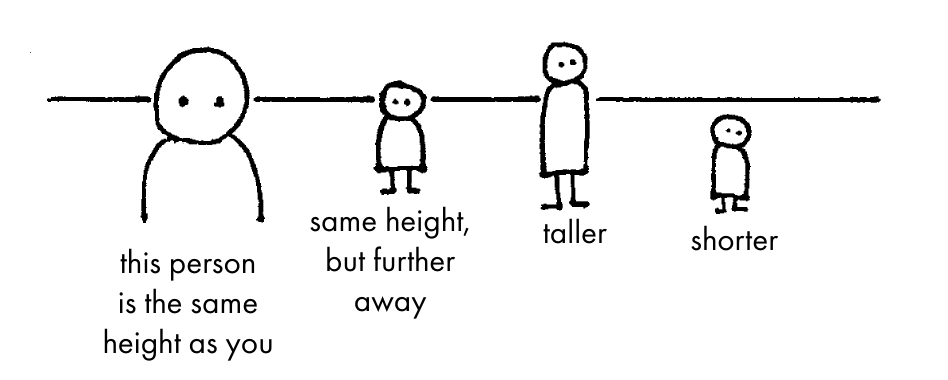
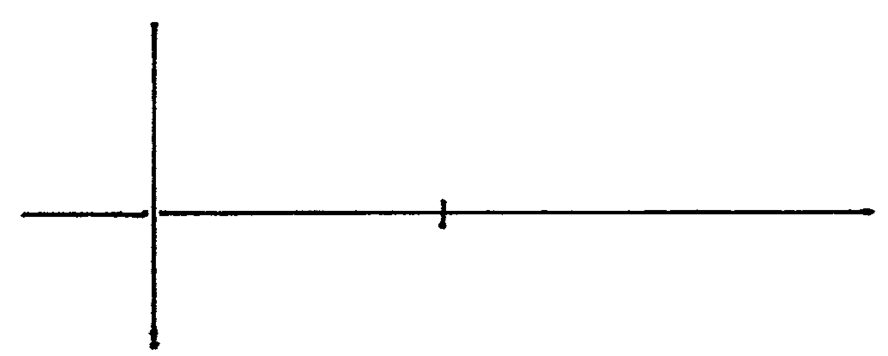
The Horizon Line

Let's begin with the humblest of all drawing elements: the horizon line.

Three boxes demonstrating height relative to a horizon line — The horizon line is **relative to the viewer's eye level**. This means that it can be used to determine the relative heights of objects.

Three simple characters demonstrating height relative to a horizon line — If a character's eyes are level with the horizon line, the character is the same height as the viewer (assuming they're standing on the same level)

A square with converging edges indicating the position of the horizon — You can use any two converging lines to locate the horizon. The point where the lines meet is where the horizon line should be.

A square with edges converging toward the horizon — Edges that run parallel to the ground always meet at the horizon line.

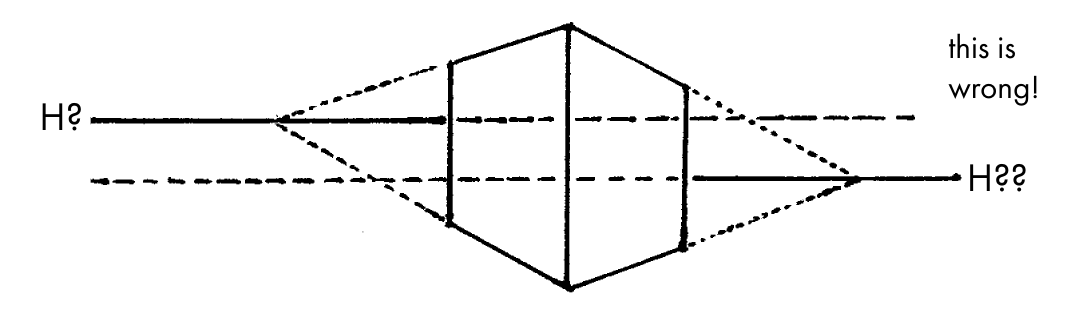
A box with edges that incorrectly converge toward two different horizon lines — It's important to determine the position of the horizon line as early as possible... otherwise you may find you've drawn angles that converge at different horizon lines:

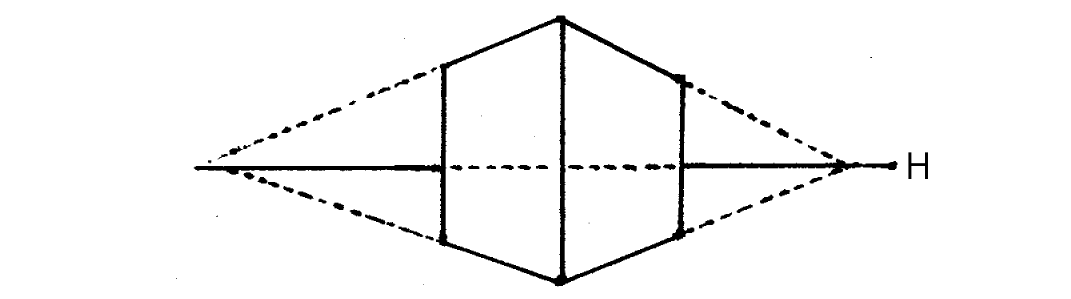
If this happens, all you can do is pick one of them, then correct the nonconforming lines. Remember: lines converge toward the horizon! There are exceptions to this which will be covered later on, but it's still the most important principle of perspective drawing.

A box with all edges correctly converging toward a single horizon line

Single-Point Perspective

A horizon line with a single vanishing point marked — Here's the horizon line again. The little mark in the center represents the vanishing point (VP).

Determining angles for single-point perspective is easy.

Let's say this vertical line represents the edge of a fence.
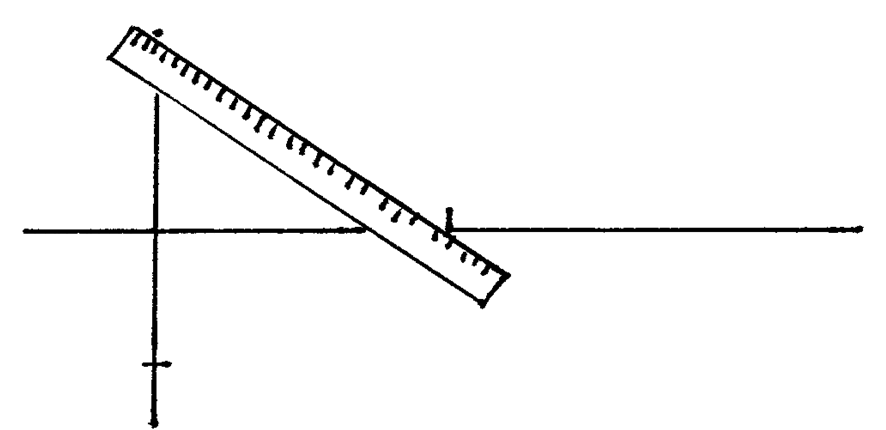
Align a ruler from the top of the fence to the vanishing point and trace the line.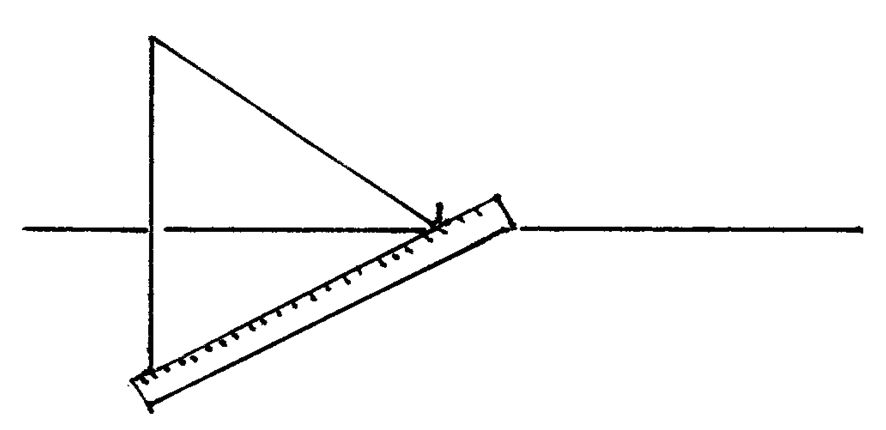
Again for the bottom.
A fence!
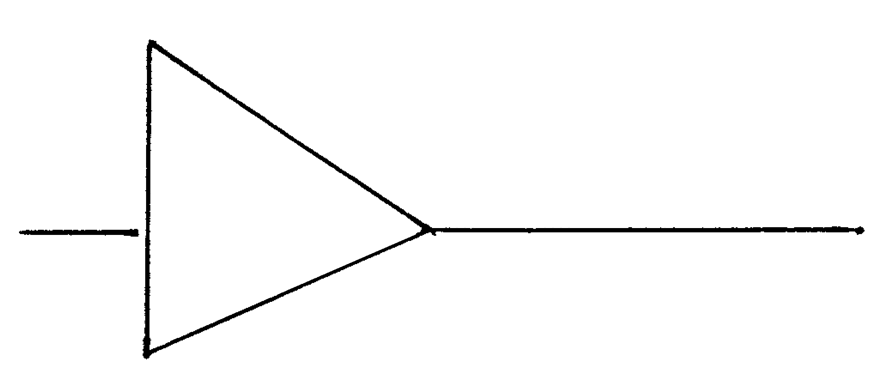
Of course, if we don't want an infinite fence, all we have to do is add another vertical and end it early.
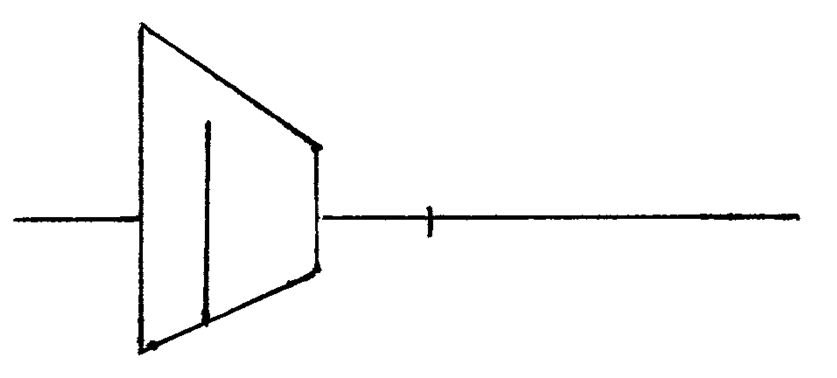
While we're at it, let's add a door to the fence. Draw a vertical line representing the height of the door.
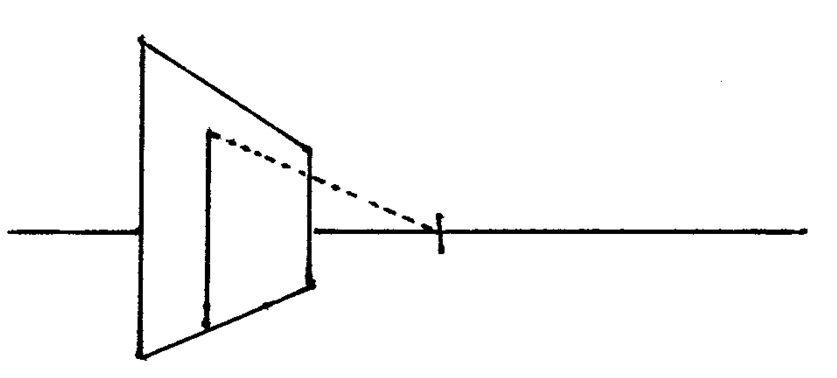
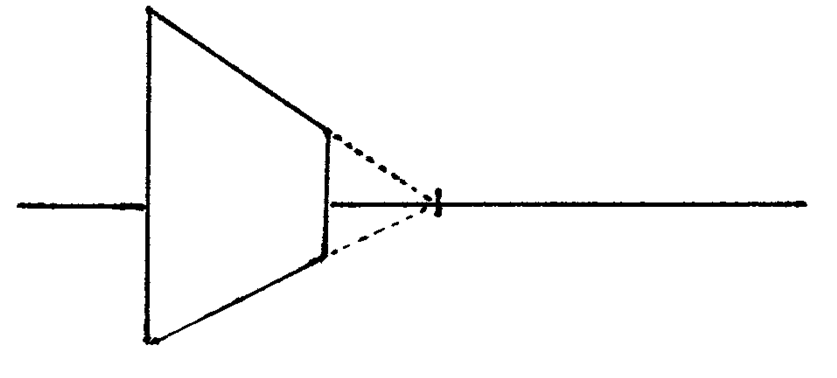
Find the line that goes from the top of this line to the vanishing point.
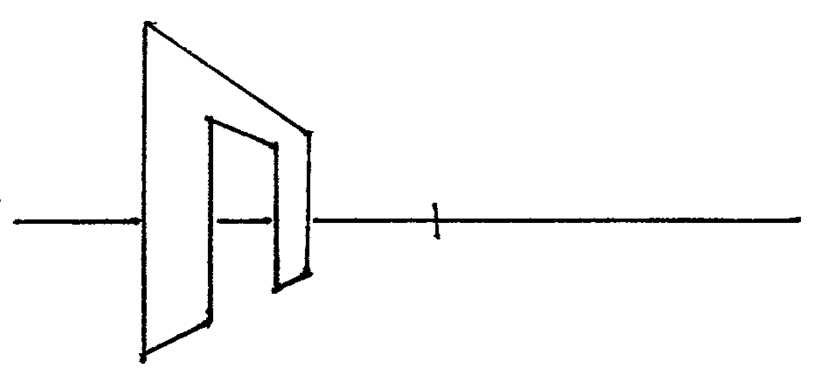
Add another vertical line and we've got a door!

A digram showing how objects can be aligned in space under single-point perspective — We can use horizontal lines to align objects in single-point perspective. In this example, the two farther doors are aligned with each other, while the two closer doors are not.

Single-point perspective is nice because it's easy. It's incredibly simple to determine any angle using nothing but a ruler.

But don't think that just because it's simple that it's useless. In fact, I would argue that you should consider it your default—why overcomplicate things? In many cases single-point perspective is all you really need.

Single-point perspective: Examples

A single-point perspective drawing from Last Look by Charles Burns — Single-point perspective can be used to direct the eye to a specific point in space. In this example by Charles Burns, the converging lines all point to the door, and the long uninterrupted edges of the planks imply the path that the character is about to take.

A single-point perspective drawing from Motel Art Improvement Service by Jason Little — Here, Jason Little uses a classic steeply-converging single-point perspective combined with a low eye level to create a dramatic and disorienting effect. This composition also draws attention toward the man with the briefcase.

A single-point perspective drawing from Ghosts by Raina Telgemeier — In most single-point compositions the vanishing point is within the frame, but this drawing by Raina Telgemeier provides a nice counterexample. The converging lines still draw the eye toward the VP, which in this case means that they "guide" the character into the open space in the upper part of the panel.

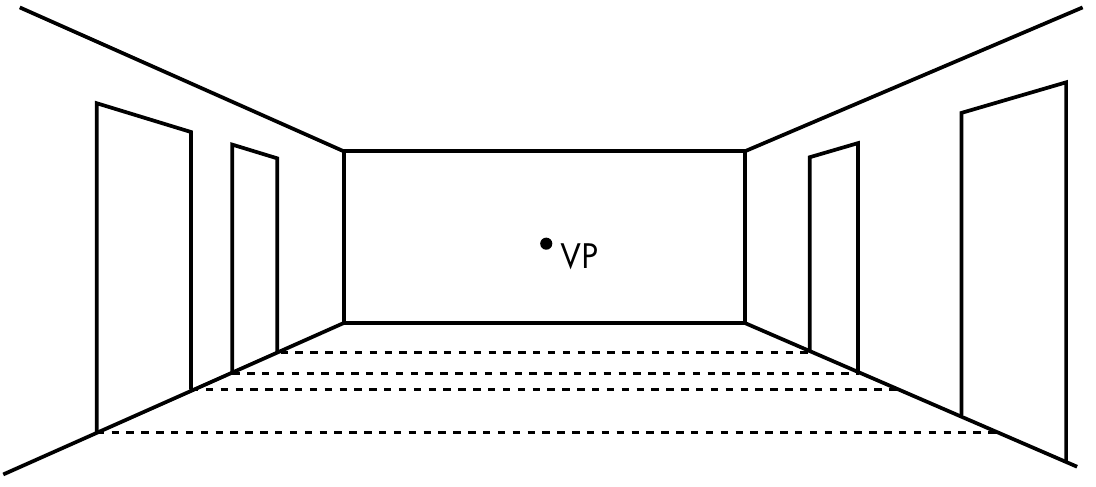
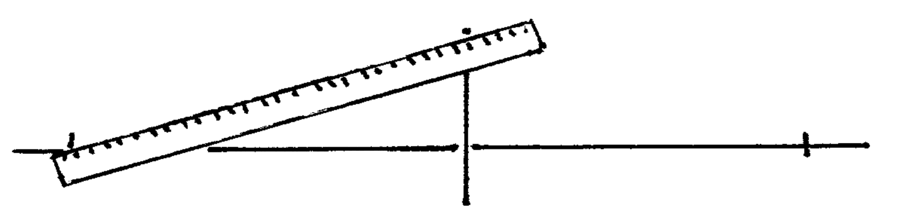
Two-Point Perspective

A horizon line with two vanishing points marked — The horizon line is back—now with two vanishing points!

Two-point perspective works much like single-point perspective, but now both left-to-right axes converge.

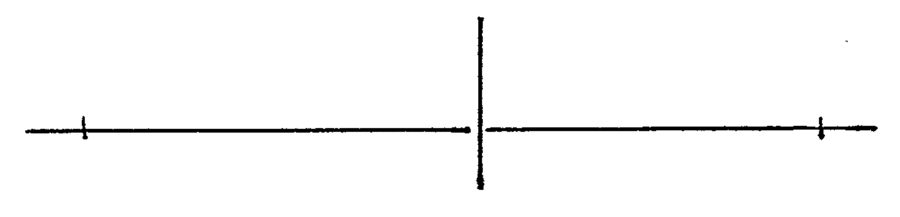
A horizon line with two vanishing points marked, intersected by a vertical line — Let's say this vertical line is the edge of a box:

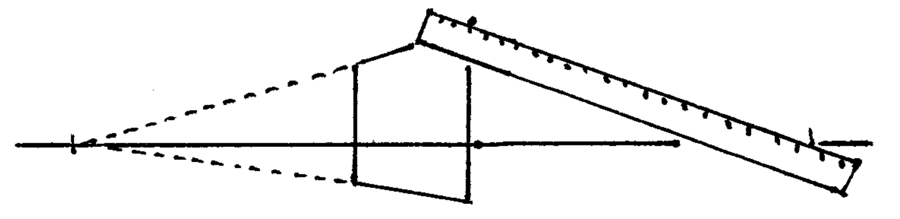
Using a ruler to find an angle for two-point perspective. — Find the angles for the left side by tracing to the left vanishing point:

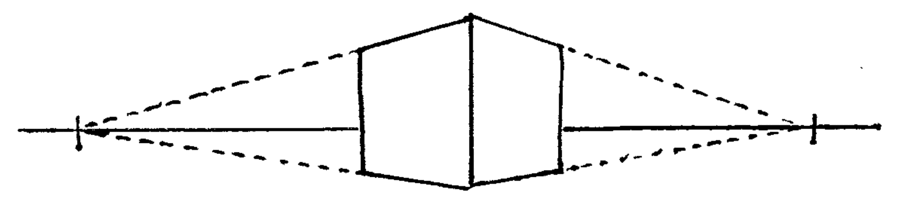
A box drawn in two-point perspective. — A box!

Two-Point Perspective: Examples

An illustration in two-point perspective from The Tinderbox by Ivy Allie — In this example from my own work, steep angles of convergence contribute to the sensation of a small, cramped space.

An illustration in two-point perspective from Cigars of the Pharaoh by Herge — Here, Hergé uses vanishing points well beyond the edges of the composition. The resulting shallow angles of convergence show that the city is still some distance away.

An illustration in two-point perspective from Berlin by Jason Lutes — Jason Lutes uses two-point perspective very effectively to create solid, believable architecture. Like the previous example, converging lines are nearly parallel, creating a "compressed" effect similar to that of a telephoto lens.

Three-Point Perspective

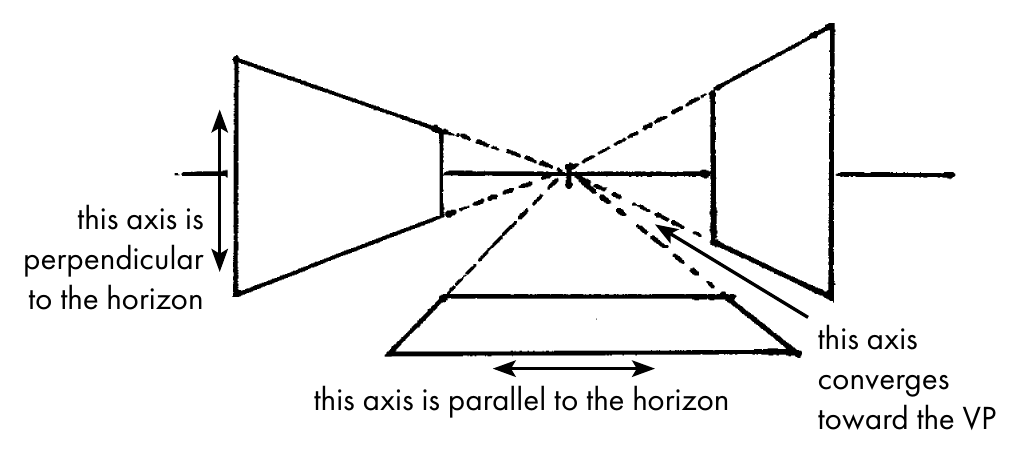
In three-point perspective, vertical lines are no longer perpendicular to the horizon. Instead, they converge toward a third point located either above or below the horizon. All three axes now converge!

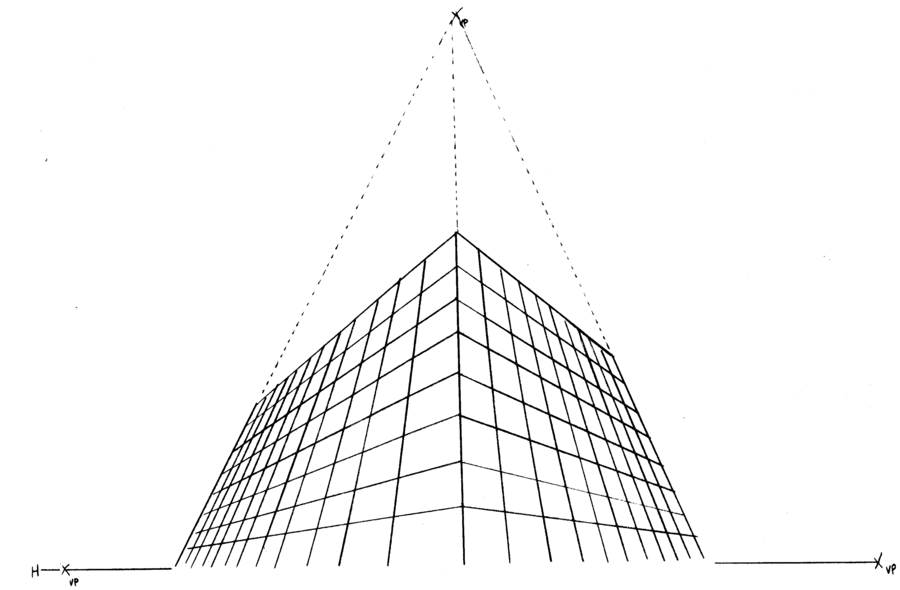
Three-point perspective is most useful when drawing a viewpoint that's looking upward or downward, especially when tall objects are involved.

But three-point perspective isn't your only option for drawing these kinds of views. Depending on the subject, you may be able to save yourself some trouble and use two-point or single-point to achieve similar effects:

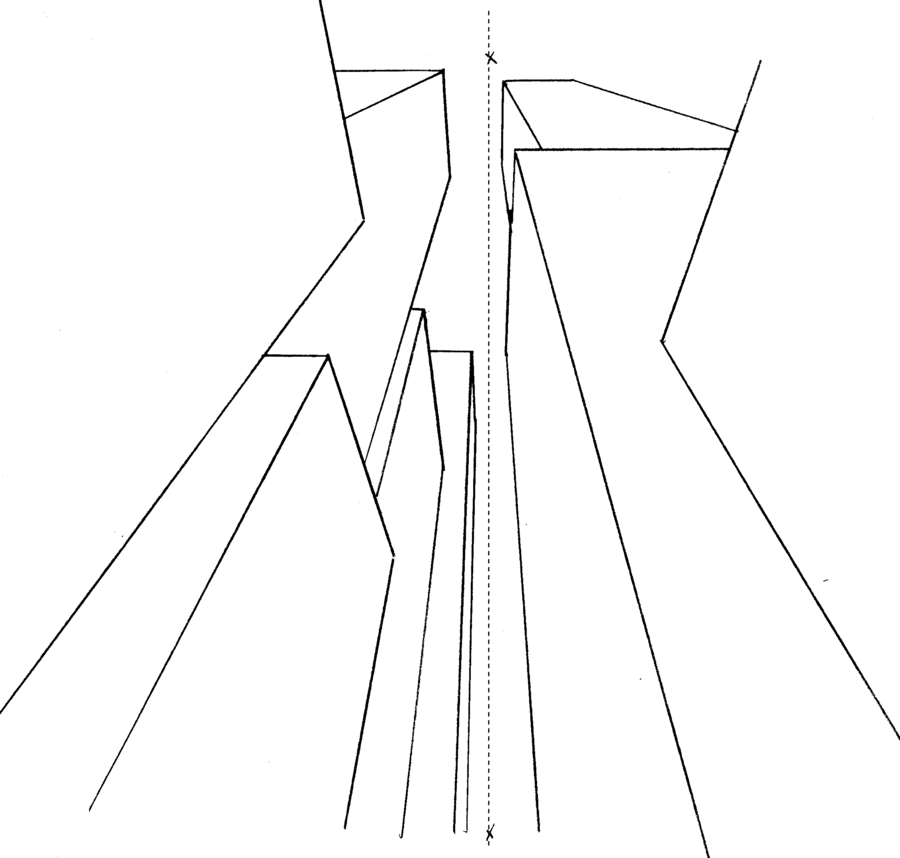
A 'fake' three-point perspective that is actually two-point — Here, a modified two-point perspective is used to create a "worm's-eye view" of a city street. Instead of converging toward the horizon, things converge toward a vertical line that runs through the middle of the composition. The two vanishing points are on this line.

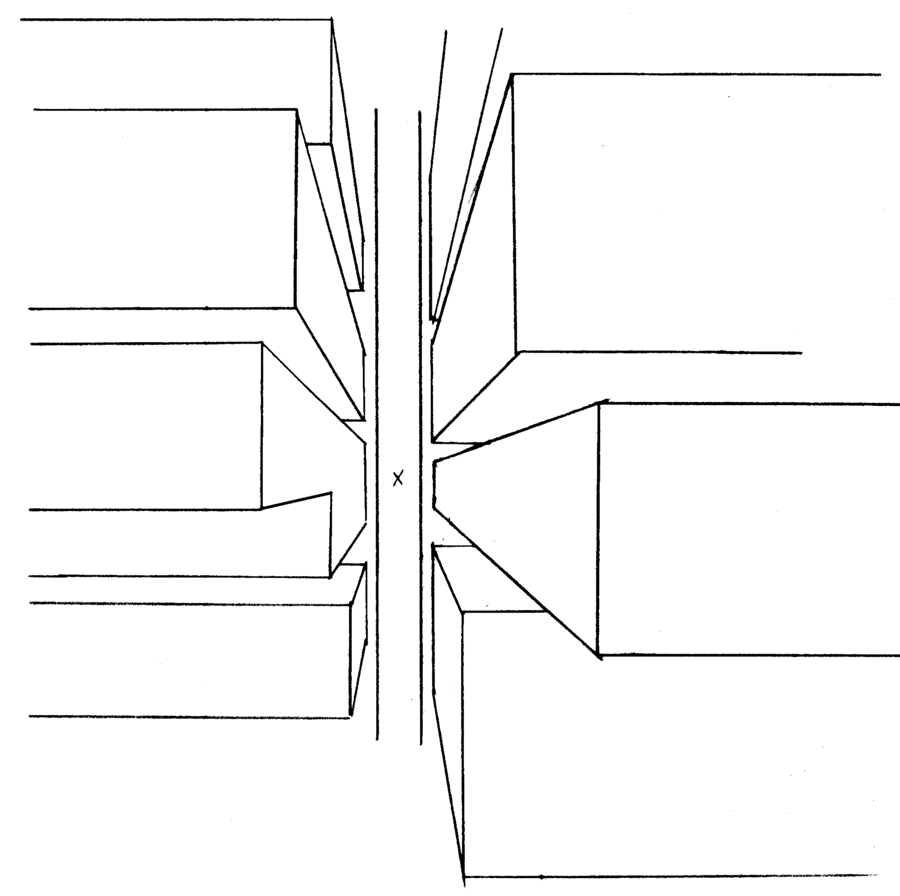
A 'fake' three-point perspective that is actually single-point — And here, the classic "looking down at the city street" effect is accomplished using single-point perspective!

Three-Point Perspective: Examples

An example of three-point perspective from I Never Liked You by Chester Brown — Chester Brown uses three-point perspective to create a dramatic sense of depth that also directs the eye toward the car. Brown's lines are drawn freehand, which makes me think he may also be finding the angles by instinct rather than defining specific vanishing points.

An example of three-point perspective from Berlin by Jason Lutes — Jason Lutes draws a top-down view of a stairwell in three-point perspective. Don't try this at home, kids!

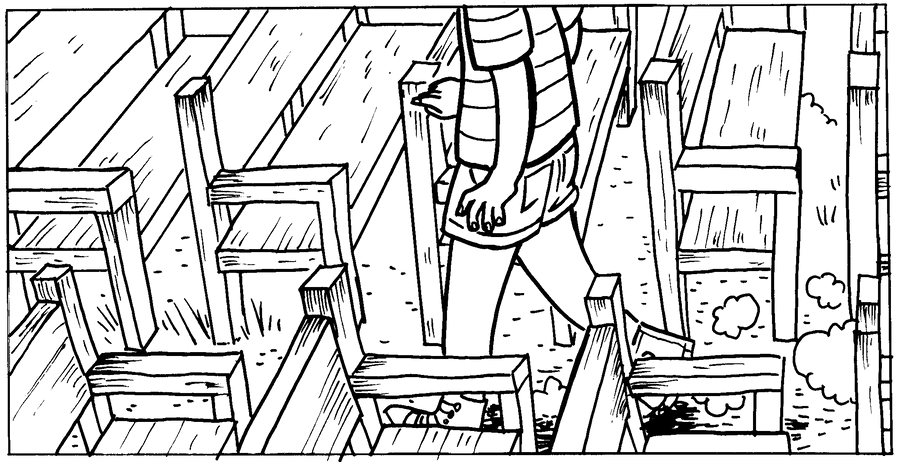
An example of 'fake' three-point perspective from Ghosts by Raina Telgemeier

Ellipses

Ellipses are circles drawn in perspective. Drawing a good ellipse isn't easy, but the principles behind them are fairly simple.

Begin with a square drawn in perspective, then add two diagonal guides to find its center.
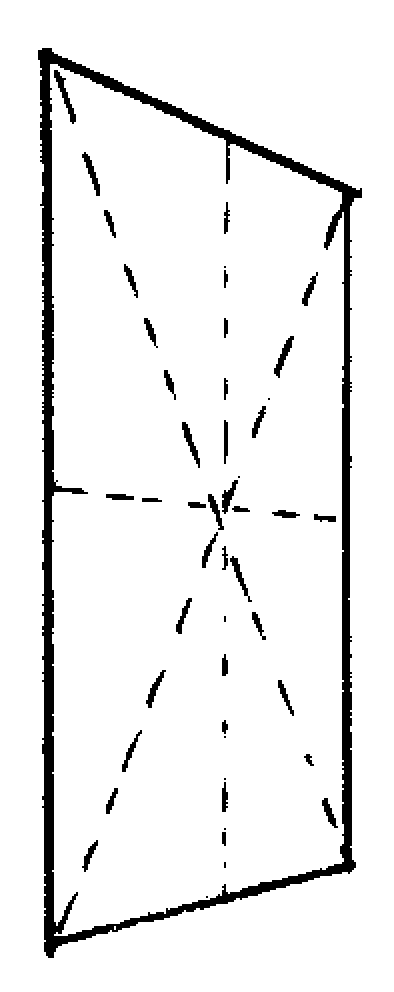
Draw vertical and horizontal guides through the center point. (Don't forget to align them with the corresponding vanishing points as needed!) The points where these lines meet the edge of the square will also be where the ellipse touches it.
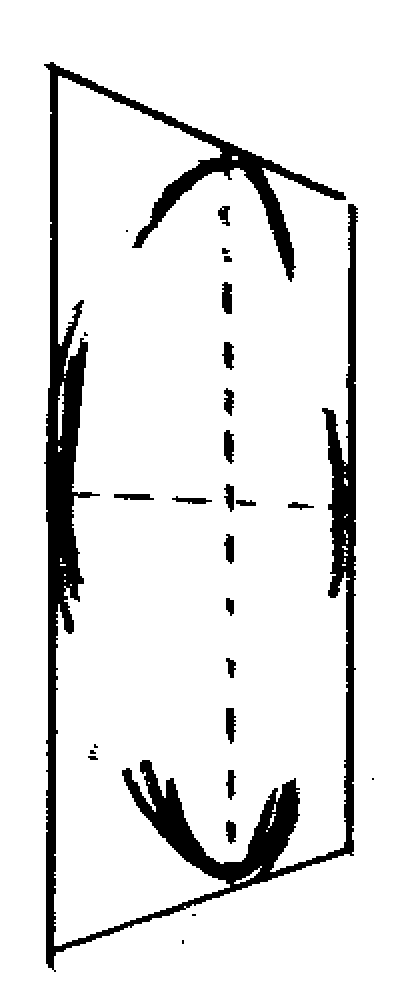
Begin sketching in the curves of the ellipse. It can be helpful to start from the guideline intersections and work from there, but it's not mandatory.
Continue sketching until you have filled out a consistent- looking curvature all around. Don't erase after mistakes, just add more marks until you have a sense of the correct form.
Note: Because ellipses are receding in space, they are not symmetrical!
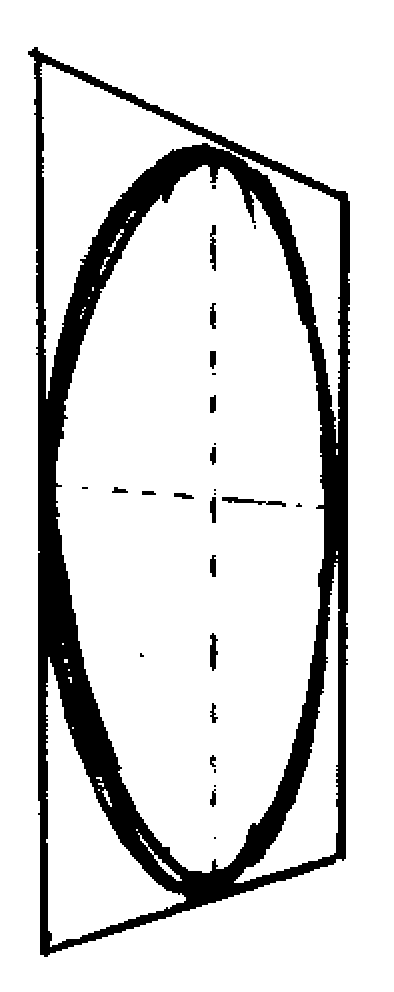
Finally, do your best to freehand an ellipse that follows the curve you worked out. It can be useful to do the preparatory work on a separate sheet of paper and then transfer with tracing paper or a lightbox.

There's no way around it—drawing ellipses is hard. My advice: don't expect to get them right on the first try. Assume that you will have to experiment and clean up. If your process includes the computer, don't be shy about using digital ellipse tools if that's what it takes. You can also buy a set of plastic ellipse templates, but they're expensive.

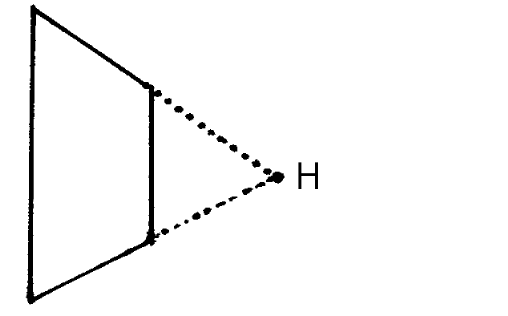
Placing Your Vanishing Points

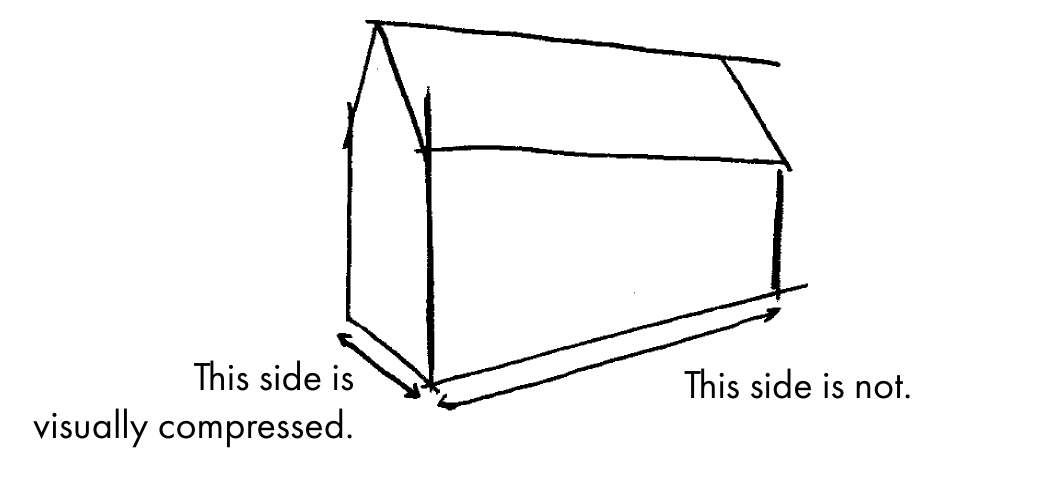
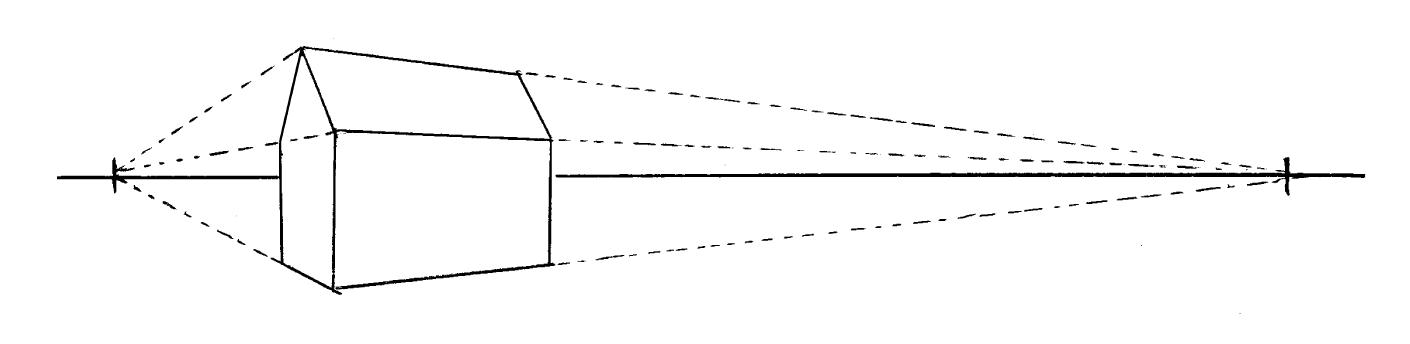
The positioning of vanishing points relative to your scene affects how space is distorted in your drawing.

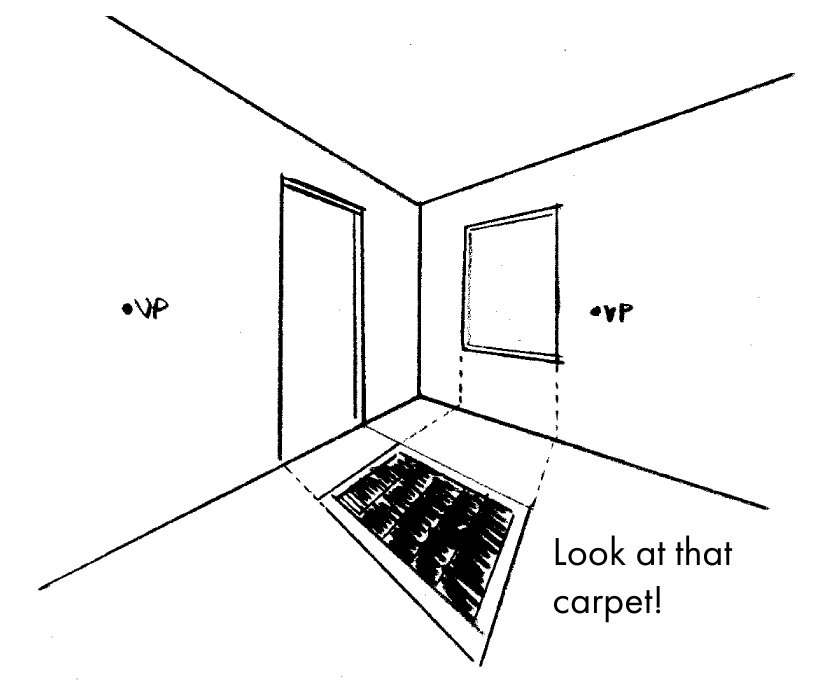
An illustration showing how distortion increases when vanishing points are close together — Points that are close together increase distortion:

An illustration showing how distortion increases when vanishing points are further apart. — Moving the left point further away gives a more naturalistic look:

(Moving the right point, or both points, would have worked just as well)

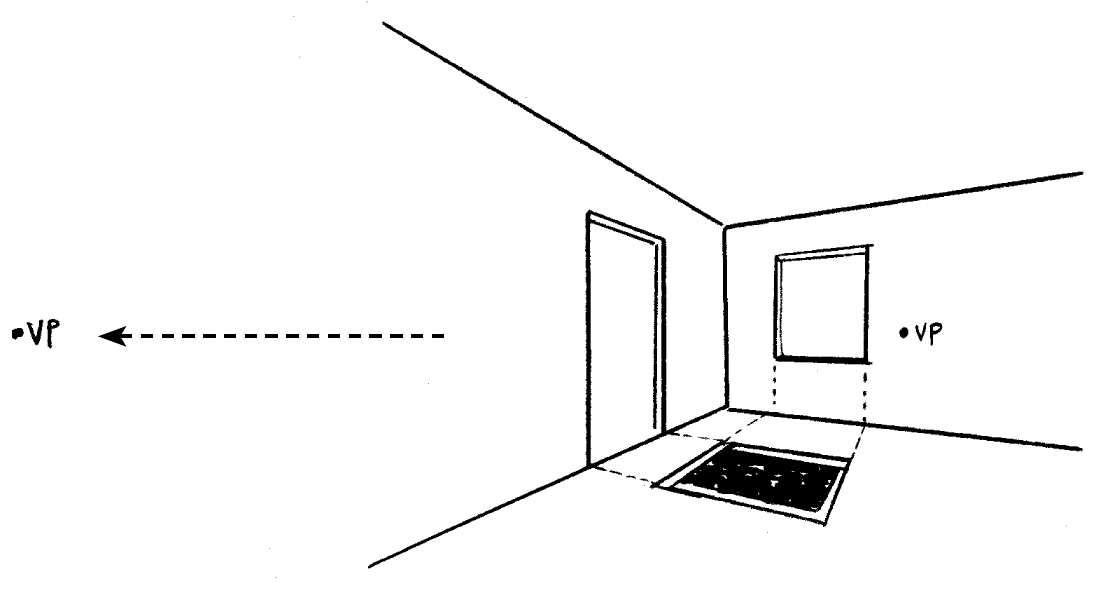
Once you know how the positioning of a vanishing point affects distortion, you can use that knowledge to estimate the vanishing points from a rough sketch.

A simple sketch used as a reference for vanishing point placement. — Let's say we want a building that looks roughly like this:

Vanishing points placed following the previous sketch as a guide. — To achieve the same effect, the left vanishing point should be close to the building, and the right vanishing point should be far away:

Just about right, but this also brings us to a recurring problem with multi-point perspective, namely:

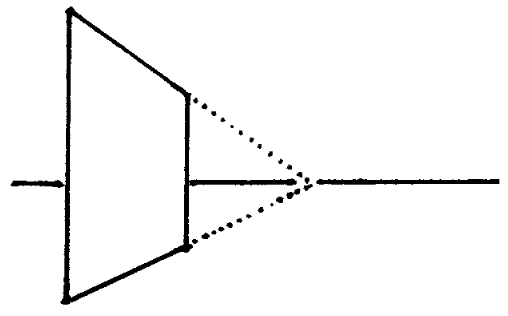
What To Do When Your Vanishing Point Is Beyond the Edge of the Page

This is perhaps the most frequent bugaboo of perspective drawing. Luckily there are a few ways to address it.

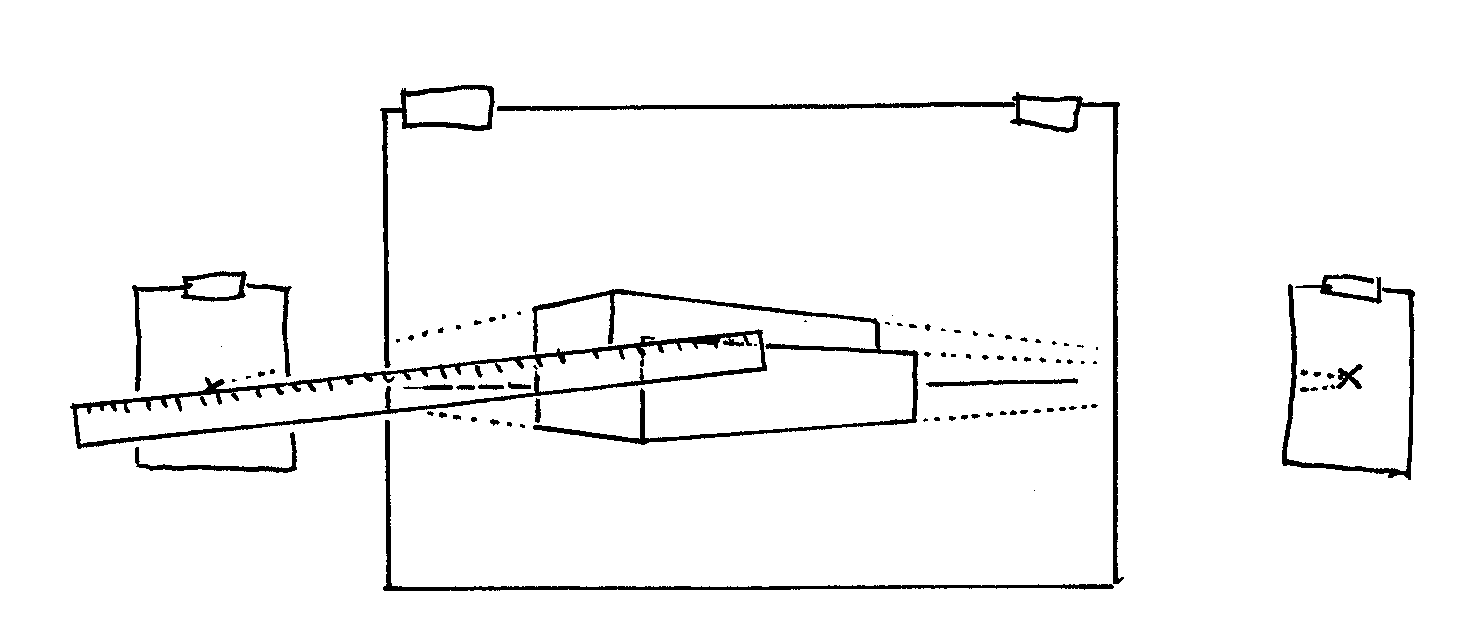
Extending your paper to find vanishing points beyond the edge. — By far the easiest method is to tape down extra pieces of paper and draw the vanishing points on them. Use a long ruler to connect the lines. Usually I find that the distances aren't so far away as to make this entirely impractical. It looks stupid and messy but trust me, if you can make this work it will make things easier for you in the long run.

Another method is to make a study drawing at a smaller size, then enlarge it once you've figured out all the critical angles. You can use a copying machine for this (and I highly recommend having a good scanner-printer in your studio).

Alternatively, you could work with a perspective grid, as seen in the next section!

Creating a Perspective Grid

Another option for situations in which the vanishing point is off the page is to construct a perspective grid to use as a guide instead. I find using a perspective grid to be more difficult than aligning directly from a vanishing point, but some people like them and maybe you will too! This technique for constructing a grid is sometimes called the Brewer Method and was popularized in the book How to Draw by Scott Robertson with Thomas Bertling.

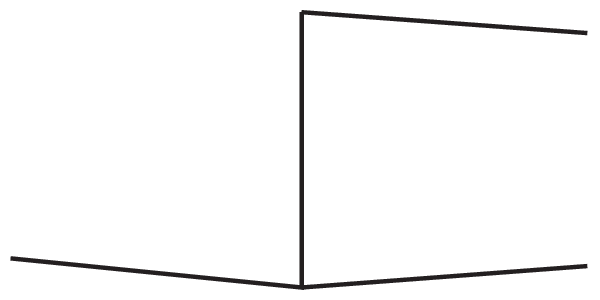
These three lines are the basis of our grid. You can adjust the angles of the lines as needed as long as the lines all converge toward a horizon. We don't know where that horizon is yet, but the two lines on the right converge somewhere. So the first step is to find the upper left line that will converge with the lower left line at the same horizon.
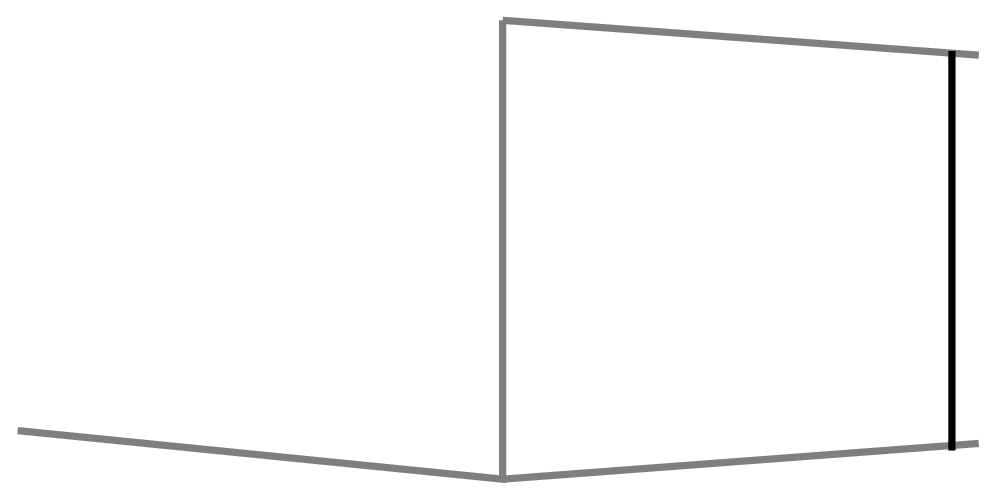
Add a vertical line between the two right-hand lines. Place it as far as possible from the other vertical line.
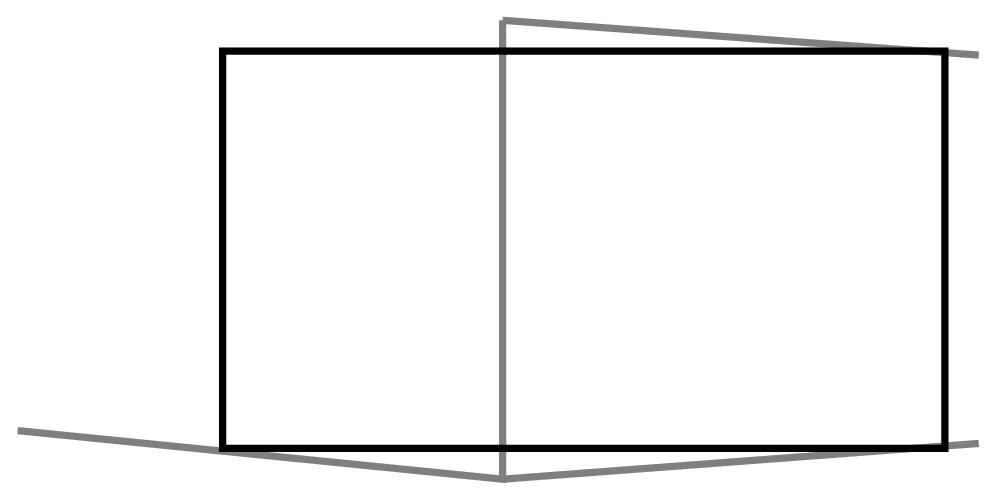
Create a rectangle using this new vertical. The lower left corner of the rectangle is placed at the point where it intersects the lower left line.
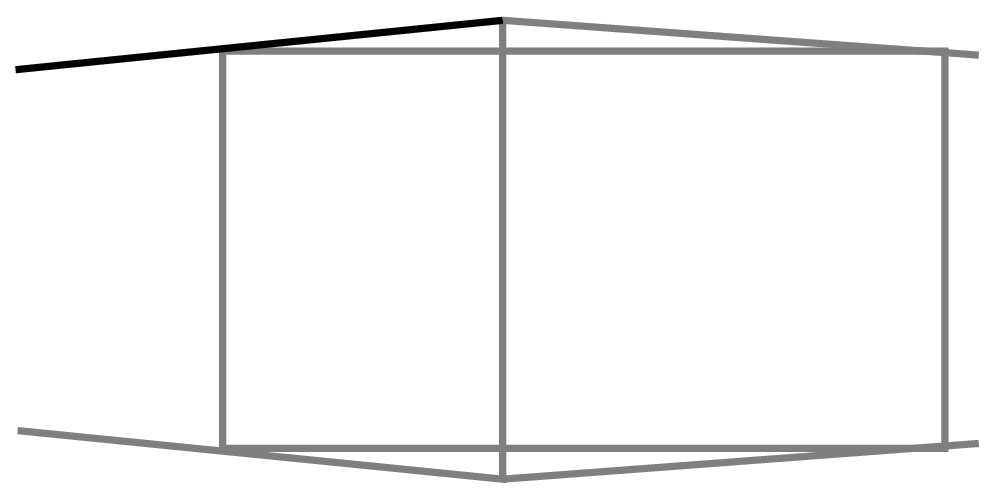
Now we know the correct angle for the upper left line –from the top of the vertical through the upper-left corner of the rectangle! Were you to extend the left and right lines, they would converge on the same horizon.
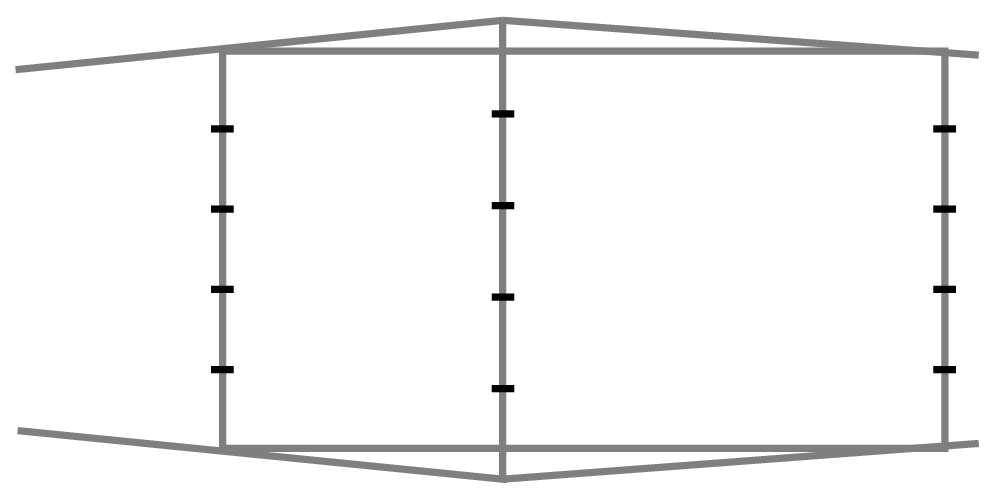
Divide each vertical line into some number of equal segments. To do this you'll need to measure the lines and calculate the length of the subdivisions. I recommend using centimeters for this operation— much easier to measure out!
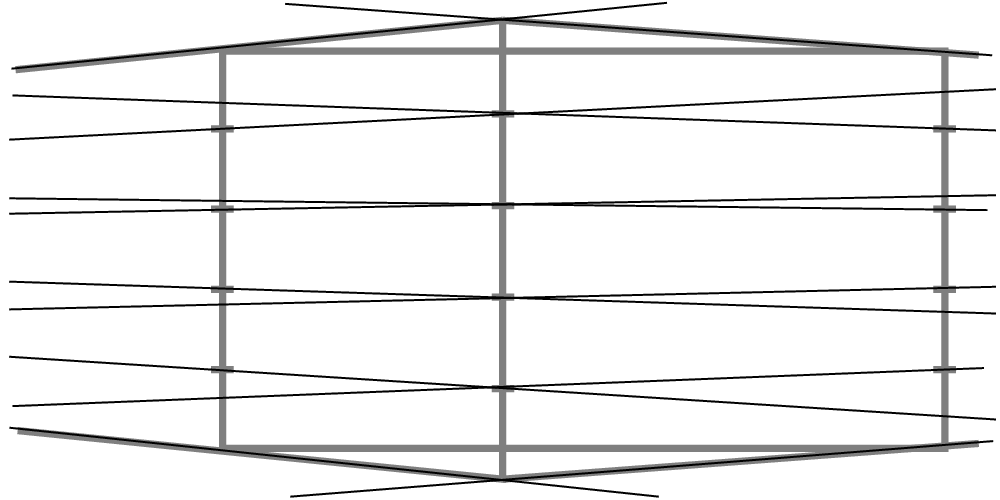
Now draw lines from the division points on the left and right verticals through the corresponding divisions on the central vertical. You've got a perspective grid! If you want to add more lines to the grid, simply make more subdivisions and repeat.

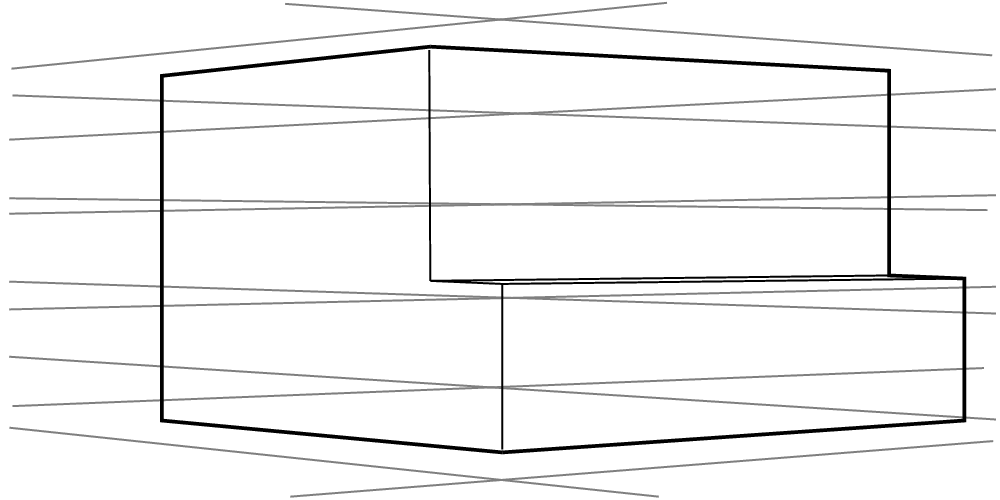
An object drawn using a perspective grid generated by the Brewer Method — The grid allows you to approximate the correct angle for any line by comparing it to the nearest grid lines. This won't be 100% accurate, but for most cases it will be good enough.

It's not a bad idea to keep the grid on one sheet of paper and your drawing on another, using tracing paper or a lightbox. This way you won't have to erase the grid from your final drawing, plus you'll be able to also reuse grids and save time!

Dividing Space

This shows how to subdivide a given space into a specific number of sections of equal size. You can use this for the boards of a fence, banks of windows, or support beams under a roof.

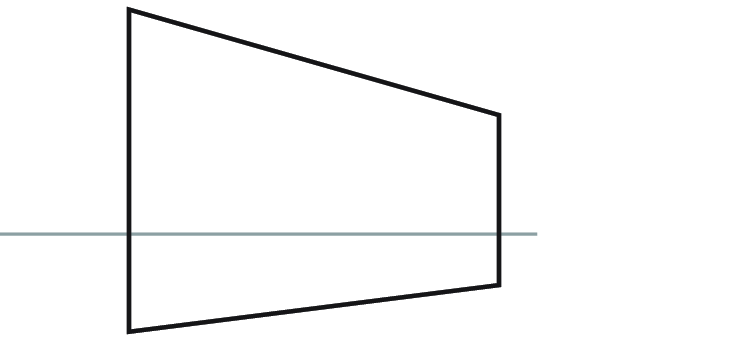
Here is a wall. Let's say we want to divide it into five segments of equal size.
First, create a series of equally-spaced points aligned with the upper corner of the geometry. To make five segments, we'll need six points. (Number of points = Number of segments + 1)
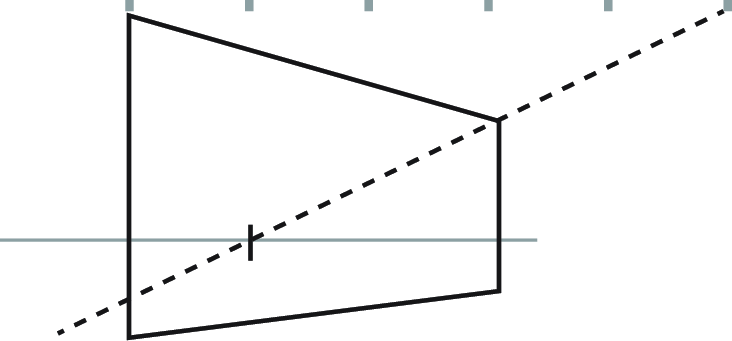
Next, draw a line from the last point through the other end of the upper edge. Where this line meets the horizon, mark a new vanishing point.
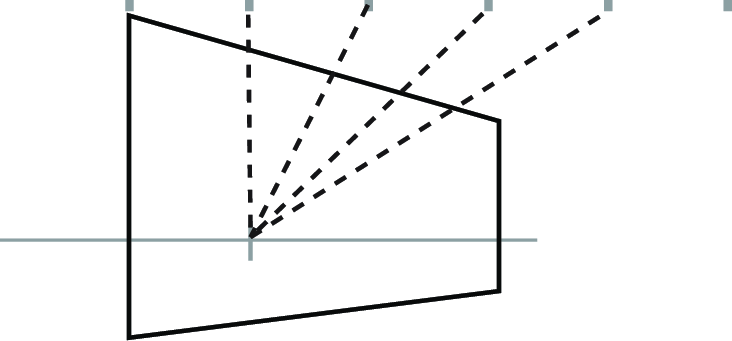
Draw lines connecting this new vanishing point to the other points of the guide.
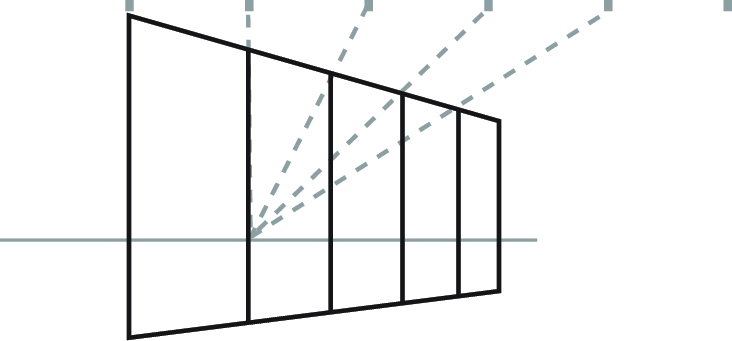
The points where these new lines intersect the upper edge are the perspective- adjusted positions for the divisions!

Multiplying Space

This shows how to repeat a unit of space an arbitrary number of times. You can use this for an array of equally-spaced objects, such as lampposts, telephone poles, or trees.

Here is a giant lollipop. Let's say we want to create a row of equally- spaced giant lollipops (and really, who doesn't?).
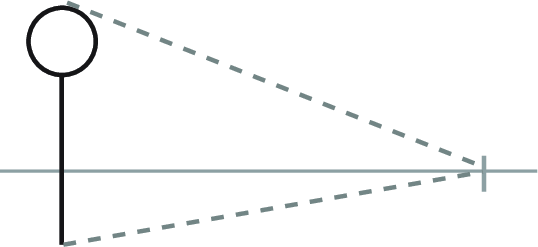
Create guidelines running from the top and bottom of the lollipop toward the vanishing point.
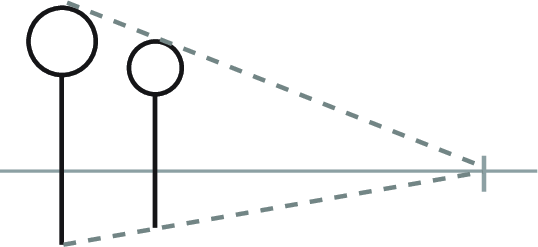
Choose the position for the next object in the series. Its position will determine the spacing for the rest of the series, so choose carefully!
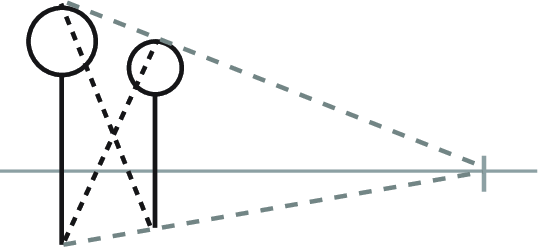
Find the center point between the objects by drawing an X between them, connecting the corners diagonally.
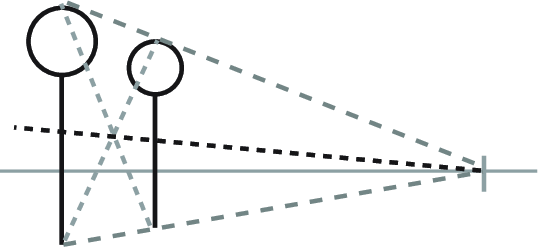
Add a line that runs through the center point to the vanishing point.
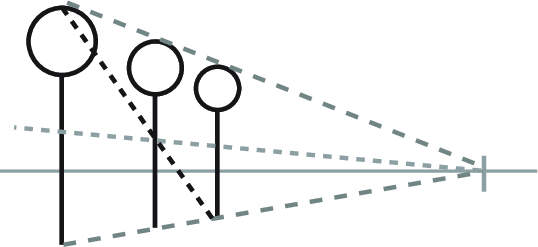
Draw a line from the top of the first lollipop through the intersection of the center line and the second lollipop. The third position is where this line meets the lower guide!
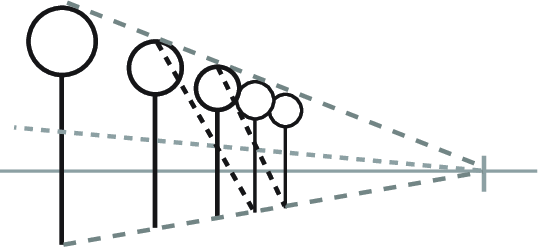
To find the fourth position, draw a line from the top of the second through the center of the third. And so on to infinity!

What's the difference between these two techniques?

Dividing is useful when you need a specific number of points to be cover a specific space. For example, if you were to draw the side of a building and you want it to have a row of equally-sized windows, you would want to divide the length of the wall to find where the windows will go.

Multiplying is useful when you need to repeat an interval of space, but the exact length and number of repetitions doesn't matter. In our row of windows example above, multiplying would not be an ideal solution, because you would need to use trial and error to find the exact width needed to make the edge of the last window perfectly align with the far edge of the wall. However, if the far edge of the wall is beyond the edge of your composition, multiplication would probably be a better choice!

In short: Multiplication is easier but harder to control. Division is more complicated, but gives you more specificity. One method is not better than the other, but they have different applications. Start experimenting with them and you'll quickly understand when to use one or the other!

Orthographic Drawing

In orthographic drawings (also sometimes called paraline drawings), lines run parallel to each other and do not converge. In general, orthographic views use vertical lines for one axis, and specific diagonal angles for the other two axes.

The most common orthographic method is isometric, in which the two "side-to-side" axes are both set at 30° from the horizontal. Isometric artwork has been widely used to create an illusion of depth in non-3D video games.

An example of isometric perspective from David Mazzucchelli's Asterios Polyp — Here, David Mazzucchelli uses an isometric view to depict an architecture classroom. Thematically appropriate!

To create an isometric grid:

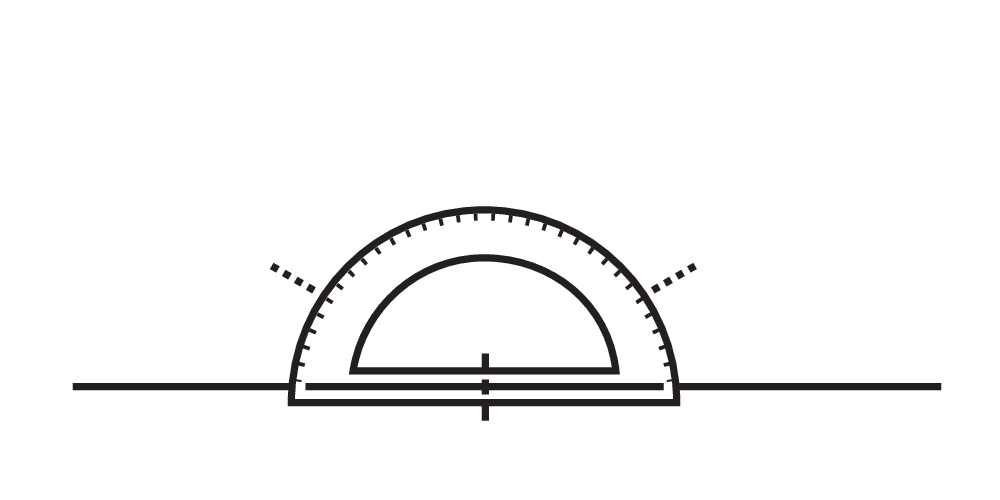
Draw a horizontal line and mark a point on it. Use a protractor to find 30° angles from this point.
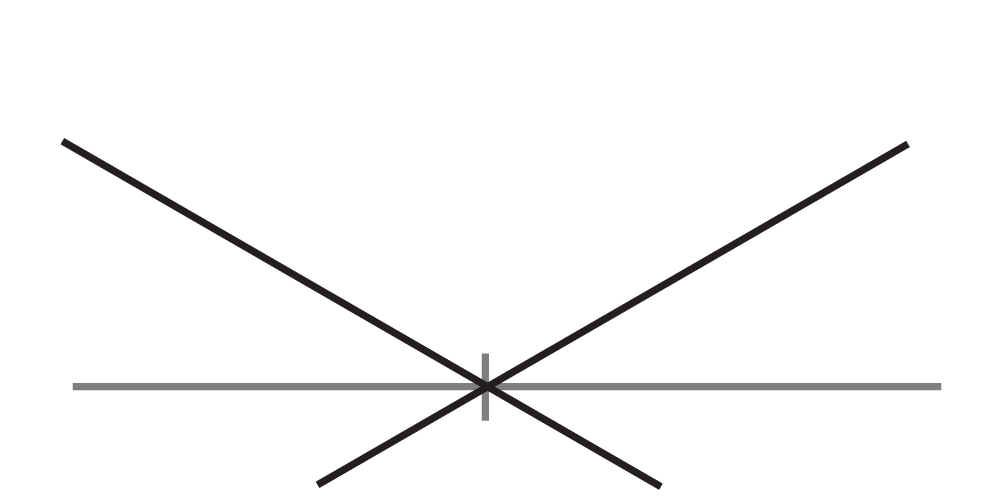
Draw the two diagonal lines that correspond to these marks.
Now duplicate the lines at regular intervals. I recommend a transparent grid ruler, or rotating the paper and using a T-square.

Orthographic drawings have inherent clarity, which is why they are often used for diagrams and architectural plans. But this also makes them a good option for comics and illustration, where clarity is often more important than "realistic" perspective. Strangely, the technique is somewhat rare in comics, but it has a lot of potential. Try it!

Faking It

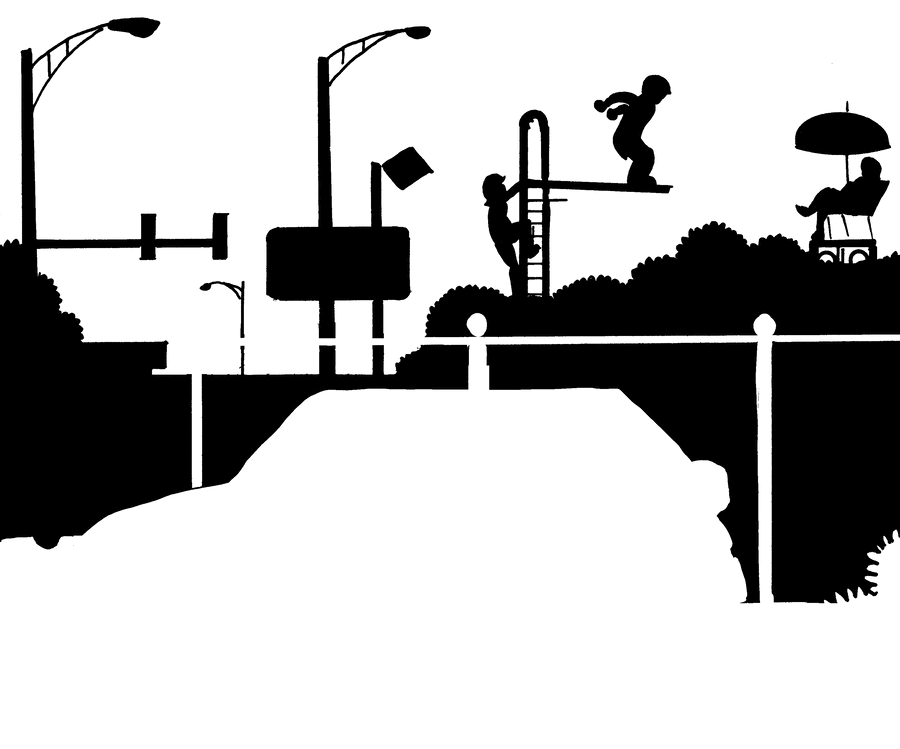
Sometimes perspective just isn't worth the trouble. I'd like to introduce you to an interesting approach to this that's frequently employed by comics artists. It doesn't have an official name that I'm aware of, but you might call it "flat perspective." This drawing by Chris Ware (master of the form) is a good example of this technique.

A drawing by Chris Ware showing "fake" perspective

Objects in the distance are smaller, but they do not recede in a mathematically predictable way.

The orientation is an orthographic ¾ view, which suggests a bit more depth than a head-on view would.

Foreground objects are emphasized with a heavier line, and are closer to the bottom of the composition.

The characters and the car both sit on a horizontal "ground line."

Below the ground line is a space that represents the surface of the ground.

This method is fascinating because it makes no logical sense, but it does make sense intuitively. Placing characters' feet on a horizontal line "feels right," even though this scene could never exist in actual space. These kinds of drawings are easy to read, and easy for the artist to construct: a perfect match for comics art!

An example of "fake" perspective from "Of Course, No One Knew" by Ivy Allie — Another example, from my own work. Notice that the floor is "sloped" to show texture but other flat surfaces (the TV table, the counter) are seen edge-on.

Two Last Things

Atmospheric Perspective

Air is not completely transparent. Even on a clear day, distant objects appear slightly faded. Atmospheric perspective uses this effect as another way to convey depth. Fading out the background also serves to diminish its visual significance, making it less likely to distract the reader.

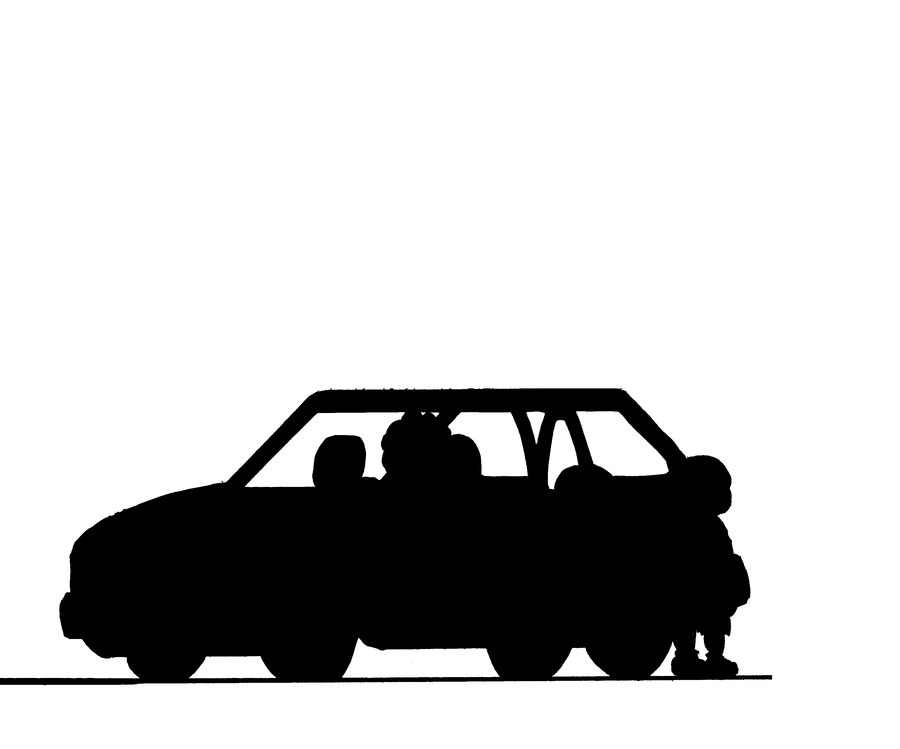
Layers of Depth

Consciously plan your compositions to have a foreground, middleground, and background. Multiple layers of depth always make a drawing more dynamic and interesting, and also offer some interesting possibilities for layout. Seen here is a breakdown of the Chris Ware drawing from the "Faking It" section into four layers. Notice how the car is framed in the image both by the bush in the layer in front of it and by the fence in the layer behind it. Consider adding another layer of depth to your next drawing—I think you'll like the result!

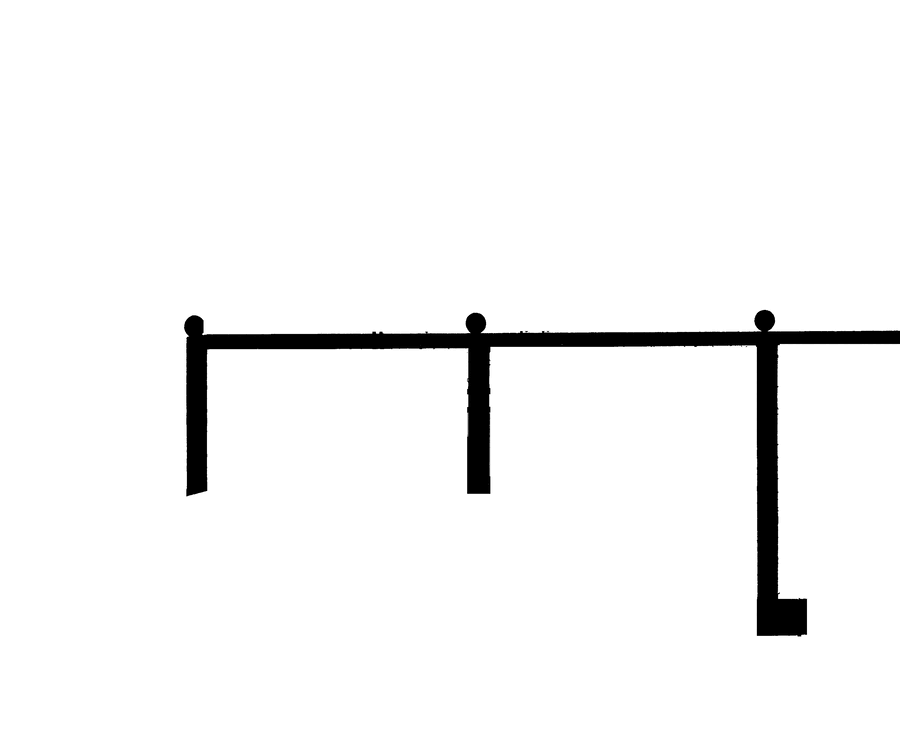
Exercises

Design a very simple building and then draw it a few different ways. Move the vanishing points around, try three-point, rotate it, do an isometric view! Do your best to keep its features consistent.
Use the same vanishing point layout to draw an interior scene and an exterior scene. Note the ways in which they feel different even though the parameters are the same.
Draw a wall in perspective and then add a row of regularly- spaced windows. There are multiple ways to do this. See how many you can think of.
Invent your own system for representing depth! This is all artificial anyway so anything is valid so long as it makes sense to the viewer.
Make up a complicated scene and commit to getting the perspective right. Pretty broad for an exercise, I know, but the best way to get the hang of this stuff is to do it a lot.

Indicia

Created in 2022 by Ivy Lynn Allie.

This content is not copyrighted. Please feel free to duplicate it, redistribute it, modify it, and spread the joys of perspective drawing wherever they are needed! (For non-commercial purposes.)

More specifically, this content is licensed under the Creative Commons Attribution- NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0) license.

The exception to the above is the artwork examples, which are subject to the copyrights of their respective owners (see below). In the context of this booklet their inclusion is considered fair use, but reusing them in other contexts may not be! Use common sense and always credit the original artist. It's also worth noting that these images are traces, modified slightly for clarity and ease of reproduction.

Art Credits

Ivy Allie, "The Tinderbox", CC BY-NC-SA 4.0 2022; "Of Course, No One Knew", ©2020; Acting Out (forthcoming), ©2020. Chester Brown, I Never Liked You, ©1991-2002. Charles Burns, Last Look: X'ed Out, ©2010. Hergé, Cigars of the Pharaoh, ©1955 Casterman, Belgium. Jason Little, Motel Art Improvement Service, ©2010. Jason Lutes, Berlin: City of Stones, ©2004. David Mazzucchelli, Asterios Polyp, ©2009. Raina Telgemeier, Ghosts, ©2016. Chris Ware, The Acme Novelty Library, ©2005.